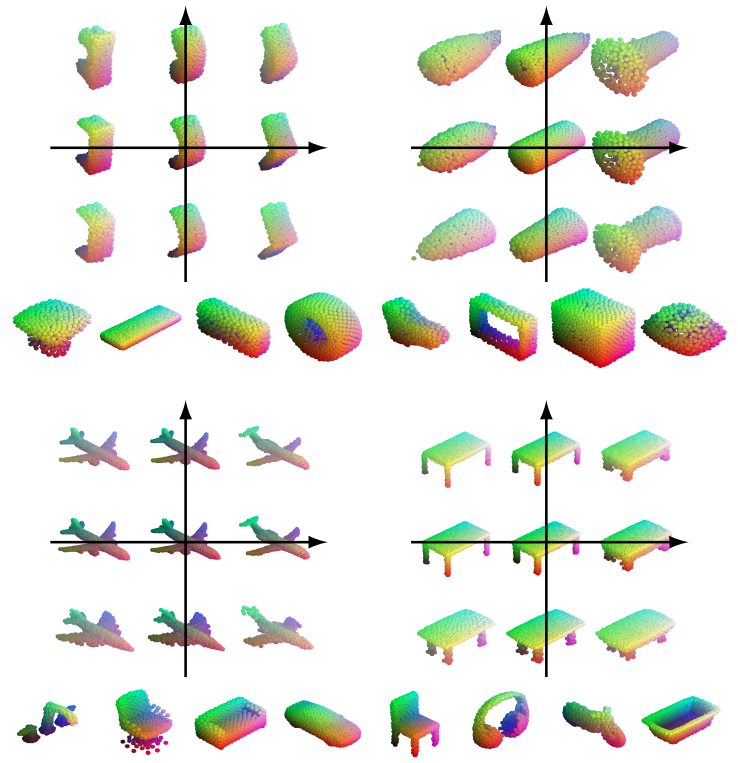
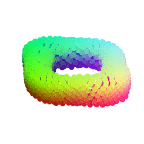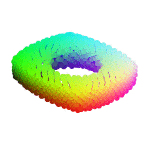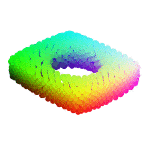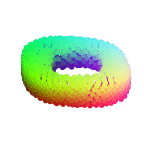Abstract¶
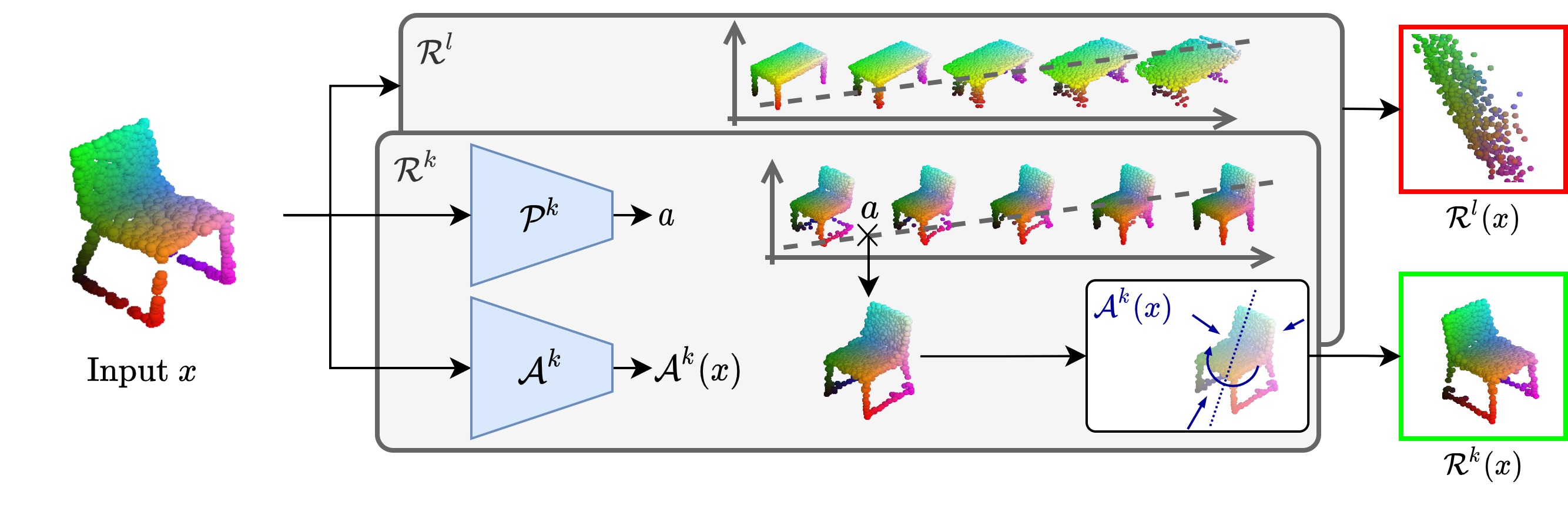
In this paper, we revisit the classical representation of 3D point clouds as linear shape models. Our key insight is to leverage deep learning to represent a collection of shapes as affine transformations of low-dimensional linear shape models. Each linear model is characterized by a shape prototype, a low-dimensional shape basis and two neural networks. The networks take as input a point cloud and predict the coordinates of a shape in the linear basis and the affine transformation which best approximate the input. Both linear models and neural networks are learned end-to-end using a single reconstruction loss. The main advantage of our approach is that, in contrast to many recent deep approaches which learn feature-based complex shape representations, our model is explicit and every operation occurs in 3D space. As a result, our linear shape models can be easily visualized and annotated, and failure cases can be visually understood. While our main goal is to introduce a compact and interpretable representation of shape collections, we show it leads to state of the art results for few-shot segmentation.
Pipeline¶
Ressources¶
If you find this project useful for your research, please cite:
@inproceedings{loiseau2021representing,
title={Representing Shape Collections with Alignment-Aware Linear Models},
author={Romain Loiseau and Tom Monnier and Mathieu Aubry and Loïc Landrieu},
booktitle={3DV},
year={2021}
}Acknowledgements¶
This work was supported in part by ANR project Ready3D ANR-19-CE23-0007 and HPC resources from GENCI-IDRIS (Grant 2020-AD011012096).

 Romain Loiseau1,2
Romain Loiseau1,2 Tom Monnier1
Tom Monnier1 Mathieu Aubry1
Mathieu Aubry1 Loïc Landrieu2
Loïc Landrieu2